
회귀(regression)
회귀란 ${y=f(x)}$라는 함수를 통해 변수 사이의 관계를 공식화하는 것을 가리킨다. 회귀에서는 ${y=f(x)}$에 대해, ${x}$를 설명변수(explanatory variable) 또는 독립변수, ${y}$를 반응변수(response variable) 또는 종속변수라 한다. 회귀분석에서는 얻은 데이터에 잘 들어맞는 ${f(x)}$를 추정하고, 2개 변수 간 관계를 구한다.
선형회귀(linear regression)
회귀식 ${f(x)}$가 1차 함수 ${y=a+bx}$가 될 때, 이를 선형회귀라고 한다. 회귀식 ${f(x)}$의 형태를 결정하는 파라미터 ${a}$, ${b}$를 회귀계수(regression coefficient)라 한다. 회귀에서도 모집단과 실제 표본의 관계를 생각할 수 있다. 이때 모집단은 ${\epsilon}$를 확률오차로 한 다음 식과 같은 확률 모형이라 가정한다.

다중회귀(multiple linear regression)
단순선형회귀모형 외에 설명변수가 여러 개 인 것을 다중회귀라 한다.
일반적으로 설명변수가 ${k}$개인 가장 단순한 다중선형회귀모형은 다음과 같이 표현할 수 있으며, ${a,b_{1},b_{2}, ...,b_{k}}$ 등 ${k+1}$개의 파라미터를 가진다.

회귀계수의 가설검정
앞서 설명한 회귀계수를 대상으로 가설검정을 시행할 수 있는데, 이 경우에는 오차 ${\epsilon}$의 분포가 정규분포라고 추가로 가정해야한다. 단, 표본크기 ${n}$이 충분히 클 때는 오차항이 정규분포를 따르지 않아도 가설검정을 시행할 수 있다.
귀무가설은 '기울기 ${b=0}$', 대립가설은 '${b\neq0}$'으로 하여 가설검정을 실행한다. 귀무가설이 옳다면 설명변수 ${x}$가 없는 ${y=a+\epsilon}$이라는 모형이 되므로, 서로 다른 설명변수 ${x}$의 값에 대해 ${y}$는 아무런 변화도 없을 것이다. 가설검정 결과 ${p<0.05}$를 얻었다면 통계적으로 ${b}$가 0이 아니라고 주장할 수 있으며, ${x}$에 대해 기울기 ${b}$인 선형관계라는 것을 알 수 있다.
최소제곱법(least squares)
회귀모형 ${y=a+bx+\epsilon}$의 가장 적절한 ${a}$와 ${b}$를 결정하기 위해서는 데이터와 모형 차이(잔차)의 제곱을 모두 더한 값 ${E}$를 최소화하는 값을 구하면 된다. 이는 ${a,b}$가 변할 때마다 달라지며 ${E(a,b)}$를 최소화하는 ${a,b}$를 구하는 것이다.

결정계수${R^{2}}$(coefficient of determination, R-squared)
최소제곱법으로 데이터에 아무리 잘 들어맞는 회귀식을 구하더라도 데이터와 회귀식이 꼭 들어맞지는 않는다. 따라서 회귀식이 잘 들어맞는지 평가하는 지표로 결정계수 ${R^{2}}$을 자주 사용한다. 1에 가까울수록 회귀모형이 데이터에 잘 들어맞음을, 0에 가까울수록 잘 들어맞지 않음을 의미한다.
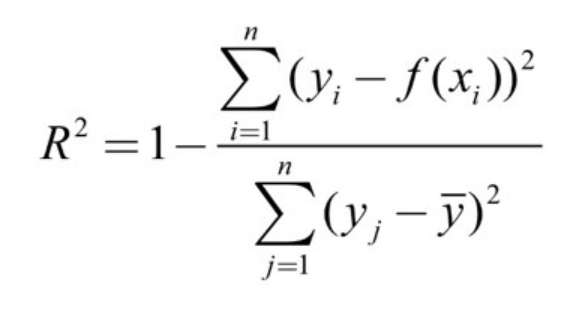
그러나 결정계수 ${R^{2}}$은 설명변수의 개수가 늘어날수록 커지는 성질이 있으므로, 의미 없는 설명변수를 도입하면 실제론 그렇지 않은데도 일견 회귀모형의 설명력이 향상된 것처럼 보일 수 있다. 따라서 설명변수 개수 ${k}$에 따라 조정한 조정 결정계수 ${R^{2}}$(Adjusted R-squared)를 사용하는 것이 일반적이다.

참고
통계 101 X 데이터 분석, 아베 마사토, 2022
https://www.udemy.com/course/statistics-for-data-science-and-business-analysis/
